首都师范大学 美术学院 孙福野
摘要:参数化设计发展至今,因其技术的优势已经广泛的应用在市场化设计项目之中,而“参数化设计”作为在数码技术应用上普及而产生的一个术语,目前还没有形成一个学术界公认的一般性概念定义,参数化的理论与参数化设计实践之间的作用关系依然处于探索阶段,没有形成完善的理论架构。可见,参数化实践的脚步已经迈在了理论的前面,当实际应用问题提出来以后又倒逼理论的发展;另一方面,在视觉设计应用中,参数化作为一种新生的创作方式也大大地丰富了视觉艺术的可能性。因此本文将对其概念进行尝试性探索和对现有理论的梳理和总结,并举例说明几类图案的绘制过程及参数化图形样式逻辑建构和预想。
关键词:参数化设计 复杂性科学理论 图形设计
中图分类号:TB47 文献标识码:A
文章编号:1003-0069(2017)11-0050-03
Abstract:Parametric design development so far is because of Parametric design’s technical advantages, and parametric design has been widely used in market-oriented design projects. But "parametric design" as a term produced in the application of Digital Technology hasn’t form a definition that accepted by the Academia. The relationship between parametric theory and parametric design practice in a state of explore, hasn’t form a complete theoretical framework. In this way, parametric practice has developed fast than it’s theory, in another word, the problems find in parametric practice accelerate the development of parametric theory. Besides, parameterization as a new way of creation also greatly enriched the possibility of visual art in the visual application. Therefore, this paper will try to explore parametric design’s concept and summarize it’s theory, and illustrate the drawing process of different graphic pattern and the construction of parametric graphic pattern logic.
Keywords:Parametric design Intricate scientific theory Graphics design
一、参数化设计概念释义
(一)参数化概念释义
什么是参数化设计?如果从字面含义来理解就是“参数”化了的设计活动,“参数”是一个变量,也叫参变量,其概念源于数学,是表明任何现象,设备或某种工作过程中的某一种重要性质的量。“参数”作为一种参变量,在系统中充当关系组织者角色,它描述系统中各个要素的组成关系和运作方式,决定了系统的变化规则;在一个动态或开放的系统中,这种参数的变化会改变系统的内在秩序,这种参数组织的关系早期源于拓扑学思想(拓扑学研究的是几何形体在连续形变之下保持不变的性质),如此来理解“参数化设计”就是基于拓扑学思想的一种设计方法。然而,参数化发展至今,通过20多年的实践,参数化得益于计算机辅助技术的发展和复杂性科学思想的影响,“参数化设计”这一词汇有了更丰富的内涵和精神。
在建筑领域中,清华大学建筑学院徐卫国教授说:“参数化设计
是把影响建筑设计的多方面复杂因素作为设计过程中的前提并综合考虑,最终以物质形态的方式来解决设计中问题的一些方法”[1] 。虽然在不同行业领域的参数化设计中其参数化对象因子不同,但参数化作为一种设计方法论和大量的计算机使用联系在一起成为了大家的共识。参数化设计的思路与传统设计不同,不再是先设定一个形态然后进行优化的过程,而是首先依照设计所要满足的重要条件,用参数语言进行描述然后在计算机的运算下得出满足条件的结果,然后在根据设计规则、美学判断以及建造可行性等优化得出最终的设计结果,这种自下而上的设计思路为设计创作提供了更多的可能性。

(二)参数化设计的两个方面
参数化设计包含两个方面,一是参数化设计思维,二是计算机辅助参数化设计技术。参数化设计思维在设计过程中要先行于计算机辅助设计,是一种将更多的设计因素参与到方案的利弊权衡中来,从而可能成为一种可以将多学科知识联系到一起的媒介,成为能将这些知识创造性地转化成全新的设计方法。参数化设计思维源于复杂性科学理论,其背后支撑是包括数学,几何学,计算机,生物学,物理学,地理学等的庞大繁杂的自然科学库,正是运用这些知识将设计向所预想的有利方向的推进是参数化设计思维的精髓所在。
计算机辅助设计是在计算机硬件和软件的支撑下,通过对设计对象的描述、造型、系统分析、优化、仿真和图形处理的研究,使计算机辅助设计师完成产品的全部设计过程,最后输出满意的设计结果和产品图形,计算机辅助设计在参数化设计中充当设计工具的角色。在设计学范畴下,参数化设计在在宏观上看是一种设计思维方式的运用,而今在微观上看它又更多地表现为一种计算机辅助设计实现的一种手段(计算机本身就是宏观上参数化的产物)。数码化设计是指在计算机辅助应用下用数码的方式来体现设计结果的方法。参数化设计与数码化设计都可能运用到计算机辅助设计,而两者的不同之处在于参数化设计应用到的软件技术能够凸显参数化思维的巧妙特质,而不是单纯的数字化呈现。
如此可见,概括来说参数化设计就是在复杂性思想和计算机辅助设计下进行的设计活动。
二、参数化设计的理论渊源
参数化设计广泛的应用在前沿的设计项目中,解决了众多设计难题并不断弥补还原论思想下的科学应用,参数化设计之所以有如此强大的力量得益于复杂性科学理论和计算机技术的高速发展。
从历史发展的角度看, 20世纪30-40年代,一般系统论,信息论,控制论“老三论”开始发迹。同时期世界上第一台电子计算机诞生;60-70年代前后耗散结构理论,协同性,突变论“新三论”及一系列非线性理论相继问世。同时期计算机辅助设计刚刚步入实用性阶段;80-90年代混沌理论、分形学、超循环理论、孤立子理论为主的复杂性科学应运而生,1984年5月,在美国成立了专门从事复杂性科学的研究机构“圣塔菲研究所”。同时期参数化设计逐渐走人人们的视野。两者在发展的阶段性上存在一定的协同,相信这也并非偶然。
(一)复杂性科学理论是什么?德国学者克劳斯·迈因策尔在《复杂性中的思维—物质、精神和人类的复杂动力学》一书中指出:“复杂性科学是一种跨学科的方法论,它是用来解释复杂系统中微观元素的非线性相互作用造成的某些宏观现象”[2] 可见复杂性科学不同于传统的纵向型学科,而是以研究方法论来界定学科的性质,正如钱学森先生所说:“凡是不能用还原论处理或不宜用还原论方法处理的问题,而要用或宜用新的科学方法处理的问题,都是复杂性问题,复杂巨系统就是这类问题”[3] 。复杂性科学以耗散结构理论、协同学、超循环理论、突变论、混沌理论、分形理论和元胞自动机理论为内核早期发展,至80年代中期之后,复杂性科学开始打破以前的学科界限,进行适应科学发展的综合研究。从其研究范围的广博性和与以往研究方法的差异性,复杂性科学已然成为了以方法论为主导的群科学。
(二)复杂性源于人类对自然的崇尚,人类不断探索自然,感受她的壮美和神秘。在设计中人们在不同的发展阶段对自然的形态和内在规律都有不同程度的效法,比如自然界中随处可见的花草树木、冰雪雨露、不断演化的山川地貌、大江大海、城市系统、各种动植物的生态系统等,但与自然本身的复杂层度相比,望尘莫及。从形式上看,自然中所有的形态都是不规则形体,几乎不存在纯粹的欧氏几何图形;从系统性上来看,所有自然生态都是非平衡态,不可逆,不确定,不可用逻辑分析的系统。但是它们遵循自然法则,具有潜在的最优化和合理性,从这种意义上看,最合理的设计应该是追求最贴近自然的状态,那么也逃不掉追随自然界的复杂性。
(三)从简单到复杂,从线性到非线性看来是人们认知发展的必然过程。1687年牛顿《自然哲学之数学原理》一书出版,奠定了近代线性科学的基础,在接下来的两个世纪里,人们依照线性的思路对规则的、确定的、平衡态的、可用逻辑分析的对象进行了不断研究,建立了线性科学的理论体系却忽略了非线性对象的研究。非线性是相对线性而言,如果自变量和因变量不具有成正比的关系,那么人们就说他们是非线性关系。自然界中非线性现象随处可见,比如一个人身高的成长:3岁时的身高60cm,5岁时身高110cm,8岁时身高130cm,11岁时身高140cm,14岁时身高150cm,17岁时身高170cm,21岁时身高175cm……等这类非正比关系都是非线性关系。非线性科学没有普适性的原理让人们使用,更多的是具体问题具体分析,比如:在数学中用牛顿迭代法解非线性方程,用动力学几何化解决非线性动力学问题。面对诸多的非线性问题,人们逐渐意识到,非线性现象才是自然界的普遍现象,非线性更接近客观事物的性质本身。线性系统不过是一部分简单非线性系统在一定条件下的近似或简化。“在非线性科学中,牛顿力学方程和统计力学法,线性随机性方程和非线性确定方程可以有机结合起来,从而达到确定性和随机性,决定论和非决定论高度的内在统一" [4] 这也正是信息时代下参数化设计的内在逻辑。

三、参数化在图案设计中的应用逻辑
从理论上来说,参数化软件可以实现任何我们想要的图形,而从操作思路上看有三种方法,第一种是直接用参数语言描述并不断地逼近所设想的图形,可能会有一种或多种参数逻辑都可以搭建出相同的图样,这就好像无论是用五笔输入、拼音输入或是手写输入都可以得到想要的文字;第二种是在实现预想图形的过程中,偶然的调整参数范围或逻辑秩序时意外的产生更优图形,这种收获正是参数时代的必然产物;第三种是根据设计要求,设定参数结构和运算逻辑,然后让计算机计算出最优解。
参数化图形的生成逻辑就好像围棋一样,只依据最简单的底层规则变化出无尽无穷的大千世界,在参数化的过程中,将所预想的图形或构建逻辑选择恰当的软件及简洁的构建方式是参数化软件运用的技术核心,比如在视觉领域,Grasshopper、Apophysis、Ultra Fractal就是较为常用的参数化图形制作软件,Grasshopper比较擅长于制作几何渐变图形,点阵图形及一些随机图形,Apophasis比较擅长于制作分形图形和类似“火焰”的有机图形。以下举例说明几类图形的制作方法。
首先以Grasshopper为例,它是更多服务于建筑领域的一款基于Rhino平台的一个插件,这款插件将复杂的程序算法打包成不同的电池图标的运算器,创作者只要将不同性质、不同数据结构的运算器按照正确的逻辑结构组合连线,就可以进行参数化的设计操作。
案例一:在曲面上绘制随机渐变图案(如图1)。
①绘制做出洞型的图元,这里的图元是四叶草形,也可以把它替换成几何图形、有机图形等图形。
②在Rhino 操作界面中选择“曲面上的内插点曲线”命令在曲面上绘制基线。
③在Grasshopper 中用曲线在曲面上偏移运算器,生成5 条等距的且贴合曲面的曲线。
④在Grasshopper 中曲线等分运算器将曲线等分成合适的段数以产生点阵(这些基点的间距可以根据设计需要设置为等相同、渐变或随机等)。
⑤在Grasshopper 中用迁移运算器将图元依次迁移到各个基点的法线平面,图元到达指定基点后就变成了新的有独立属性的图形,我们将这些新图形称之为实例图形。
⑥在实例图形之间彼此建立角度随机旋转关系、大小随机渐变关系。在grasshopper中用搭建“角度随机旋转运算器组”如电池图中的紫色组块所示。
⑦在Grasshopper中用搭建“大小随机渐变运算器组”如电池图中的绿色组块所示。并调整参数,直至图形位置符合设计意图。
⑧利用Grasshopper 中向量投影运算器将实例图形映射到曲面上,并将这些图形烘焙到Rhino空间。
⑨在Rhino中用切割命令将这些实例图形与曲面分割开来并删除,然后导出文件即可(如图2)。
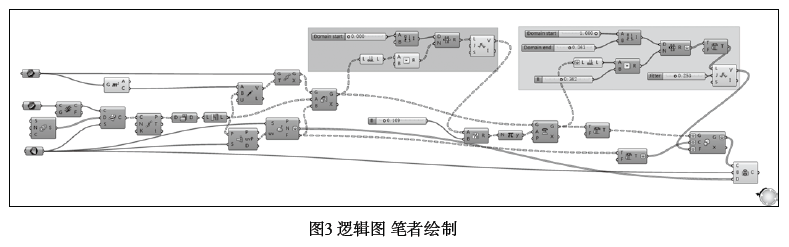
此类在曲面上建构立体图形的方法可以用于平面设计中的三维表现,例如在LOGO墙上表现不动角度渐变的LOGO底纹,也可以用这种立体构建的方式设计带有丰富图形三维的装置(如图3)。
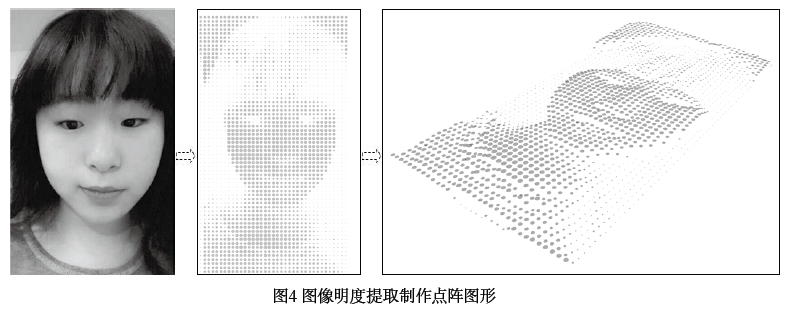
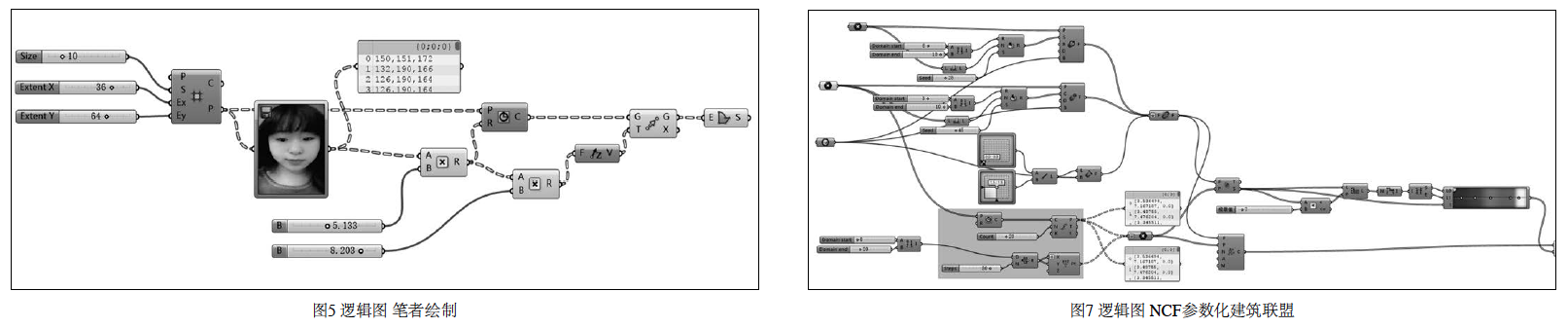
案例二:根据图像的明度作为干扰数据制作立体点阵图形(如图4)。这一案例主要用到了点阵运算器、图像采样器、乘法运算器、圆形生成器、Z轴向量坐标运算器、移动运算器、边界面生成运算器和数据拉杆输入运算器。
在Grasshopper中操作步骤如下:
①在Params菜单中拉取图像采样器(Image Sampler)至操作界面,再选择图像导入该运算器并选择明度渠道。
②用点阵运算器输出给图像,将输出端的数值通过乘法运算器调整至适宜的大小再输入给圆的半径,此时会出现(图2)中的平面图样。
③用圆的输出端和z轴向量运算器的输出端输入给移动运算器,再将移动运算器输出给便捷生成运算器即可。程序全图(如图5)所示。
此类图像采样的方法可用于图像的抽象化处理,提取图像的明度或色彩参数作为干扰因素作用于图形逻辑的搭建,再进行艺术手法的处理就可以形成形式统一、自成秩序的图形。
案例三:彩色线形“烟花灿烂”(如图6)
这一案例以多色彩渐变运算器、穿越多点之间的区域线运算器为主,搭建了这个色彩丰富,线条流畅,过度均匀的线状图形。电池逻辑搭建(如图7)。
以上案例可以体现在Grasshopper中绘制如渐变图形、干扰图形、随机图形、迭代图形等复杂的图形的快捷和可控的特性。Grasshopper虽然
如此强大,但在分形图形的创作中Apophysis软件探索得更加深入。
Apophysis是一款运用IFS迭代函数系统通过改变编码的参数来生成图形的参数化软件。创作者可以通过结合不同的函数与图形的变化规律生成层次丰富、色彩绚丽、结构精美的图形。
意大利女艺术家Chiara擅长制作分形艺术(Fractal Art),其中很多作品均是由Apophysis与Photoshop混合使用创作而来(如图8、9)所示。
参数化图形设计正在走出萌芽,走向成熟的进程中,毋庸置疑的是越来越多的参数化图形将会用在更多的领域中,例如在书籍装帧、海报招贴、广告宣传等印刷品的设计中,在装饰画、瓷砖图形、壁纸等建筑装饰的设计中,在网页界面、UI设计、影视动画等新媒体的设计中都会有广泛的应用,尤其在防伪码图形的设计中参数化图形更具有发展潜力,因为如果没有原始的逻辑代码和参数,相同的图形是无法再现的。
参数化软件凭借自身具有较强的迭代能力在快速的进化,它的应用逻辑会不断复杂多元,单独一位设计师不可能掌握所有的建构逻辑,但在设计师可以站在前人的肩膀上迅速的拿来使用。这就好像数字人像修整技术,在2000年左右,最畅销的图像编辑软件photo刚刚被更多的人用于修整图像,随着智能手机的崛起,在不到十年的时间里大量的人像修整APP开始出现,可以实现模式化的一键快速人像修整,时至今日,几乎每一款智能手机在拍照的同时就自带美颜功能。这样的发展路径将会在参数化软件的发展历程中再次出现,根据人们的设计图形倾向算法将不断改良,并一步步走向智能。
结语
参数化思维正在重新整合设计格局,计算机辅助系统也正在掀起一场设计革命,这股潮流中视觉设计工作者需要正确认识复杂性科学理论,不卑不亢地将参数化技术练成一把设计利器,以此去开启设计的新面貌.
参考文献
[1] 徐卫国 . 参数化设计与算法生形 [J]. 世界建筑 ,2009-08:110
[2] 克劳斯迈因策尔 . 复杂性中的思维——物质、精神和人类的复杂动力学.北京.曾国屏 译 [M]. 中国编译出版社 ,1991(1):12
[3] 徐国志 . 系统科学 [M]. 上海 . 上海科技教育出版社 ,2000:299
[4] 魏诺,周恩毅 . 线性科学与非线性科学哲学思想研究 [J]. 西安建筑科技大学学报 ,2008-09 (3):27
[5] 尹志伟 . 非线性建筑的参数化设计及其建筑研究 [D]. 清华大学硕士学位论文,2009.
[6] 黄欣荣 . 复杂性科学方法论:内涵、现状、和意义 [J]. 河北师范大学学报 ,2008-04,(31) :81
[7] 黄献明 . 复杂性科学与建筑的复杂性研究 [J]. 华中建筑 ,2004-04 (22) : 21
[8] 马志良 . 建筑参数化设计发展及应用的趋向性研究 [D]. 浙江大学硕士学位论文 ,2014
[9] 茹天 . 参数化设计对视觉图形的启示 [D]. 西安美术学院硕士学位论文 ,2013
[10] 李晋尘 . 参数化图形设计分析 [D]. 西安美术学院硕士学位论文 ,2014
